The Impact of Pension Spiking
While much has been made of the impact of pension “spiking,” it is helpful to quantify just exactly how much pension spiking will cost taxpayers, and how ill-prepared an otherwise adequately funded pension account is for this practice. In the two sets of examples below, the same assumptions and the same analytical model is used as in the previous post “What Percent of Payroll Will Keep Pensions Solvent?“; 30 years working, 25 years retired, pay in real dollars doubling between the hire date and the retirement date, and various rates of return.
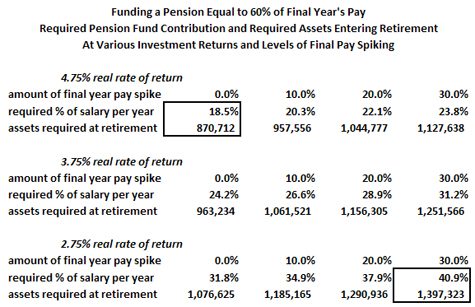
In this analysis, each block of data has three rows. The first row shows the amount by which the final pay is “spiked,” i.e., increased by a disproportionate amount through a large pay raise, cashing in of accumulated sick time, or other methods that increase pay more than it would ordinarily increase. The second row shows how much would have to be set aside as a percent of payroll each year and contributed into the employee’s pension fund, in order to ensure the fund would have sufficient assets to pay out the calculated retirement pension for 25 years. The third row puts this another way, by showing how much money would need to be in the employee’s pension fund at the time they retire. There are three sets of three rows, representing the results under three different return on investment scenarios; a 4.75% rate of return over the life of the fund (after adjusting downwards for 3.0% inflation), which is CalPERS official rate of return, along with most other public employee pension funds, then a 3.75% real rate of return, then a 2.75% real rate of return. One is encouraged to remember that a 2.75% “real” rate of return equates under these assumptions to a 5.75% actual, or nominal return. To keep this in perspective, the risk-free 10 year treasury bill earns a 3.0% annual rate of return.
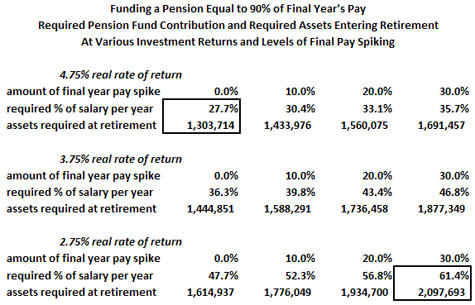
In the example immediately below, this model is applied to calculate the impact of a 10%, 20% and 30% spiking of final year pay (columns 2, 3, and 4) for a public safety employee, retiring after 30 years with a pension equivalent to 90% of their final year of pay. The baseline case of zero spiking is provided in column one. This analysis is not to suggest that all public safety workers, who represent about 15% of California’s roughly 1.85 million state and local government workers engage in spiking, or, for that matter, that the other 85%, the “non-safety” government employees in California, engage in spiking. Pension spiking is a reality that is pervasive in some agencies and jurisdictions, and nonexistent in others. In some cities and counties in California it is having a dramatic impact on pension fund solvency and the rates of contribution necessary to compensate for it. The purpose of this analysis is not to identify where and when spiking is occurring, only to quantify how much it costs when it does occur. The worst case example of spiking used here of 30% is not unusual.
To understand the above table, compare the 2nd row in each three-row block of numbers, starting with the case that uses a 4.75% real rate of return for the pension fund. The impact of an employee collecting a pension equivalent to 90% of their final pay who successfully increases their final year of salary by 30%, in order to increase their pension by the same amount, is to require their employer to contribute not 27.7% of their salary into a pension fund every year for the entire 30 years they work, but 35.7%. That is, when an employee collecting a 90% pension manages to spike their final salary by 30%, it means an additional 8.0% of salary would have had to have been contributed to their pension fund every year for their entire 30 year career working. Referring to the 3rd row in each three-row block, one can see that the impact of a 30% final year spike in pay is to require the pension fund at the time of retirement to have nearly $1.7 million accumulated, vs. $1.3 million in the baseline case.
The next table provides this same information for non-safety government employees, in cases where after a 30 year career they collect a 60% pension. This would represent pretty much the absolute lowest pension a state or local government employee in California might expect after 30 years. Teachers, for example, after 30 years of service are eligible to apply a 2.5% factor to the number of years they worked, which equates to a pension equivalent to 75% of their final salary. In this example, again referring to the first three-row set of data, which represents our best case, since it utilizes CalPERS official 4.75% real rate of return on invested funds, without spiking, the employee would have to contribute 18.5% of their pay into their retirement plan for 30 years, and would have to accumulate $870K at the end of their career in order to fund a 25 year retirement. If they manage to spike their final year of pay by 30%, they would have had to contribute 23.8% of their salary into their retirement plan for 30 years, and they would have to amass $1.13 million in their retirement fund by the end of their career.
 These examples indicate that the impact of spiking is dramatic. Whenever a government employee exploits loopholes in their pension formulas and rules in order to spike their final year’s pay, there is a huge cost to taxpayers. Referring to the charts again, if a retiree earning a 90% pension only spikes their final year of pay by 10%, their payroll contribution for the 30 years they worked would still need to have been increased by nearly 2.7%. If they spike their final pay by 20%, their payroll contribution for the 30 years they worked would need to have been increased by over 5.4%. In many cases, just these relatively small amounts of spiking, 10% and 20%, spell a required increase to the annual contribution to the pension fund that is greater than the entire amount they themselves contribute via payroll withholding. The taxpayer pays nearly everything.
These examples indicate that the impact of spiking is dramatic. Whenever a government employee exploits loopholes in their pension formulas and rules in order to spike their final year’s pay, there is a huge cost to taxpayers. Referring to the charts again, if a retiree earning a 90% pension only spikes their final year of pay by 10%, their payroll contribution for the 30 years they worked would still need to have been increased by nearly 2.7%. If they spike their final pay by 20%, their payroll contribution for the 30 years they worked would need to have been increased by over 5.4%. In many cases, just these relatively small amounts of spiking, 10% and 20%, spell a required increase to the annual contribution to the pension fund that is greater than the entire amount they themselves contribute via payroll withholding. The taxpayer pays nearly everything.
A final disquieting observation can be had by referring to the two boxes in each example, one in the upper left corner of the data set, and one in the lower right corner. The boxed datapoints in the upper left indicate how much is typically set aside for pensions based on the official projected real rate of return, 4.75%, and zero spiking of final salary. In the case of the 90% pensioner, 27.7% of payroll must be set aside, and at retirement those accumulated set asides, plus interest, must equal $1.3 million. In the case of the 60% pensioner, 18.5% of payroll must be set aside, and at retirement those set asides, plus interest, must equal $871K. But what happens if both pension spiking occurs, and the pension fund is required – by the intervention of reality – to lower their projected real rate of return for their funds by 2.0%, down to a real rate of return of 2.75%, or a nominal rate of return of 5.75%? The compounding effect of these combined outcomes is truly frightening.
In the case of the 90% pensioner who spikes their final salary by 30% at the same time as the pension fund reduces their long-term earnings projection to 2.75%, instead of setting aside 27.7% of payroll each year, they would have had to set aside 61.4% of payroll each year. Instead of accumulating $1.3 million in their pension account by the year of their retirement, they would have had to accumulate $2.1 million.
In the case of the 60% pensioner who spikes their final salary by 30% at the same time as the pension fund reduces their long-term earnings projection to 2.75%, instead of setting aside 18.5% of payroll each year, they would have had to set aside 40.9% of payroll each year. Instead of accumulating $871K in their pension account by the year of their retirement, they would have had to accumulate $1.4 million.
This is not an extreme scenario. While pension spiking is not pervasive, it is common. And anyone who thinks the worst case investment returns contemplated here are unlikely – a nominal return of 5.75% – needs to consider how long public sector pension funds that manage over $3.0 trillion in assets can continue to rely on hedging and other high-risk Wall Street tricks to outperform the risk-free rate of the 10 year U.S. Treasury bill, which is only 3.0% per year. Pension spiking causes dramatic increases to the amount necessary to fund pensions all by itself. When viewed in combination with what may well be an inevitable reduction in the projected rate of return for pension funds, pension spiking can play a material role in making an extraordinarily challenging situation even worse.

Edward Ring is a contributing editor and senior fellow with the California Policy Center, which he co-founded in 2013 and served as its first president. He is also a senior fellow with the Center for American Greatness, and a regular contributor to the California Globe. His work has appeared in the Los Angeles Times, the Wall Street Journal, the Economist, Forbes, and other media outlets.
To help support more content and policy analysis like this, please click here.

Leave a Reply
Want to join the discussion?Feel free to contribute!